Instructions for Star Count Observation

GOAL: Estimate the number of stars visible in the sky.

The idea is to count all the stars that are visible in a small but known angular field of view (in this case, a tube from a toilet paper roll) and then extrapolate this number to cover the whole sky.

The idea is analogous to counting all the sheep in 1 square mile of New Zealand countryside: multiply by the number of square miles in New Zealand to estimate the number of sheep in New Zealand.

Find a site that is as dark as possible - a really light-polluted sky is no fun.

STEP ONE: Estimate Limiting Magnitude

There are many many faint stars but only a few bright stars. For our numbers to make sense, we have to be counting the number of stars brighter than some limit . We will use the Big Dipper as our yardstick.

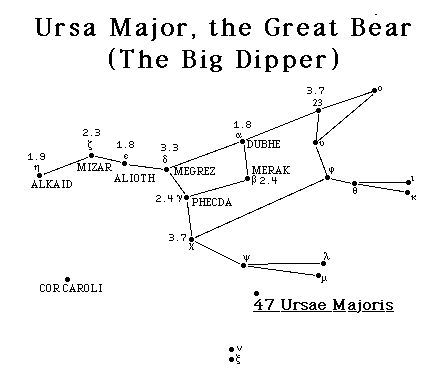
Compare the two pictures below. The second is a zoomed version of the first. (The first image is courtesy of Chris Dolan's constellation page. ) As you may recall, the magnitude scale starts with the brightest stars as magnitude 1 and the faintest stars visible as magnitude 6. Some magnitudes are marked next to big dipper stars.

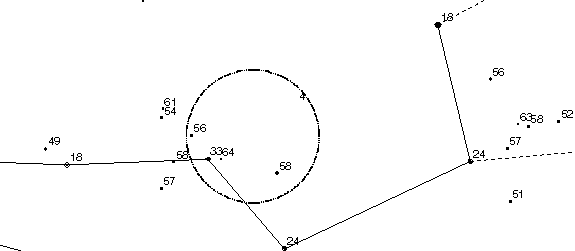
Next to each of the stars below is a two-digit number. These are star magnitudes less the decimal point, so that "24" really means "magnitude 2.4" and so on. Looking carefully through your tube, can you see any of the fainter stars? By looking at the magnitude numbers, try to estimate the magnitude of the faintest star that you can see. For instance, if you can see "Megrez" but not star 23, your limiting magnitude is somewhere between 3.3 and 3.7.

STEP TWO: Count Stars

Before you begin counting, consider the following: (1) At low altitude (the number of arc-degrees you are looking above the horizon; 0 is on the horizon, 90 is straight up) there is often a lot of haze. So don't count stars at lower than, say, 35 degrees altitude. (2) You will want to take multiple counts and average them together, so make a data grid with (for instance) altitudes of 45, 60, and 75 degrees for rows, and N, S, E, and W directions for columns. (3) Most people find it impossible to hold the tube perfectly steady. You might find it useful to tape the tube to a long stick or other convenient object. If there are only one or two stars in the field of view this is less important.

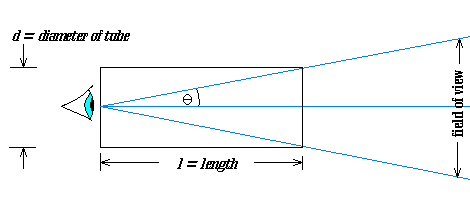
STEP THREE: Geometrical Correction

After you have an average number of visible stars as seen through your tube, you will need to multiply by a substantial correction factor to estimate the number of stars in the whole sky. The geometry is like this:

Variations on the theme:

• You might want to try this with binoculars. You need to know the field of view of the binoculars (this is often written on the binoculars themselves). Estimating the limiting magnitude may be difficult because you may see stars significantly fainter than the ones on the maps I have provided.
• You may want to try this (a) with the moon less than 50% illuminated, and (b) with the moon nearly full, and contrast the two results.
• You also may want to try (a) in, and (b) out of the city, to gauge the effects of sky darkness.