The Cafe Ellipse at Schiphol Airport, Amsterdam

Introductory Astronomy: Ellipses

(And you'd better not confuse ellipses with eclipses!)

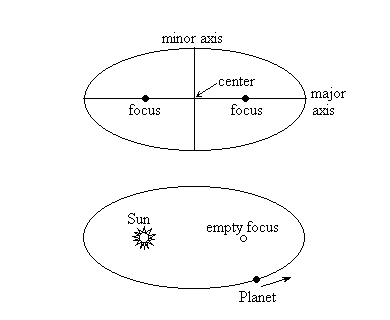
Kepler's first law is that planets orbit on ellipses with the sun at one focus. An ellipse is (sort of) an oval shape, with two interior points called foci (singular: focus), a long axis (the major axis), a short axis (the minor axis), and a center (which should under no circumstances be confused with a focus). Half of the major axis is called the semi-major axis, and the semi-major axis is also the average sun-planet distance. Kepler's first law also works for other two-body situations where one body outweighs the other by a large factor, like (1) the earth-moon system, (2) the Jupiter-Jupiter's moons system, and (3) any sun-planet, sun-comet, sun-asteroid system.

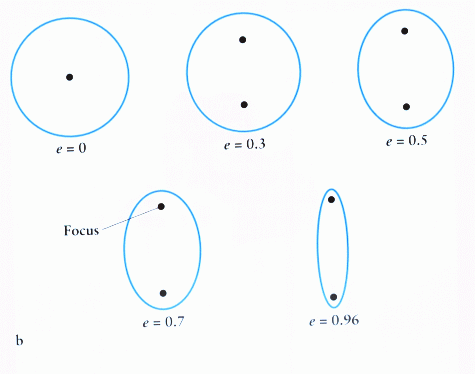
Ellipses are a class of mathematical shapes. The circle is the special case of the ellipse that happens when the two foci (and the center) are co-incident. The number that characterizes how flat the ellipse looks is called the eccentricity, denoted by the letter e. The eccentricity e can be calculated by taking the center-to-focus distance and dividing it by the semi-major axis distance. The limiting cases are the circle (e=0) and a line segment line (e=1). Below is a picture of what ellipses of differing eccentricities look like.

Important ellipse numbers:

a = the length of the semi-major axis

b = the length of the semi-minor axis

e = the eccentricity of the ellipse. e² = 1 - b²/a².

Important ellipse facts:

The center-to-focus distance is ae.

The major axis is 2a.

Perihelion and aphelion (or perigee and apogee if we are talking about earth) are the nearest and farthest points on the orbit. These points are on the major axis, as are both foci and the center. The perihelion distance is a(1-e) and the aphelion distance is a(1+e). For example, the Earth's eccentricity is 0.017 and its semimajor axis is 1.000 A.U., so its perihelion distance is (1-0.017)a, or 0.983 A.U. Similarly, Earth's aphelion distance is 1.017 A.U.

---