Introductory Astronomy: Stonehenge

Goal: In this lab we will design Stonehenge-like monuments for different latitudes on Earth, thereby understanding how the sun appears to move throughout the year. These sheets also contain questions that should be answered in the writeup. Materials: solar-motion demonstrator, scientific calculator, ruler, protractor.
Today, Stonehenge is a broken stone ring 30 meters in diameter made of hewn blocks that mass between 25 and 50 tons each. The blocks were transported from Marlborough Downs, some 20 miles north of the Stonehenge site. The ring is called the "sarsen ring" and over half of its component blocks were quarried away sometime in the centuries between 2100 B.C. and today. Archaeologists have partially reconstructed some 16 of them, and 6 are now re-capped with their lintels. There is also an inner, horeshoe-shaped arrangement of 5 lintel-capped pairs called "trilithons". The whole arrangement is surrounded by a low earthwork embankment 100m in diameter with only one gap, to the northeast, in which direction lies another boulder known as the "heel stone". (That's not the heel stone in the upper part of the above picture, but one of four "station stones".)
The purpose of Stonehenge is astronomical. It is carefully aligned so that, if one sits at the center, one has a clear view of the summer-solstice sun rising over the heel stone. Such monuments are fairly common, such as Nabta or Karnak in Egypt, Teotihuacan in Mexico, Moose Mountain in Saskatchewan, Medicine Wheel in Wyoming, or scores of stone rings found in Britain and western Europe.

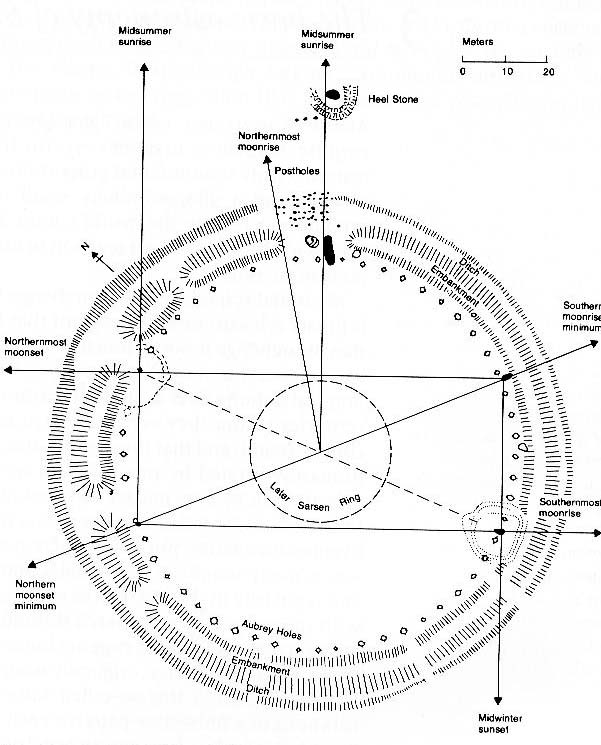
Upon 20th century archaeological inquiry, it was discovered that the Stonehenge just described was one of several versions constructed on the site. The first (Stonehenge I) was built in 2400 B.C., and appears to have been by far the most practical. The Stonehenge we see today is Stonehenge III, and seems to be more of a monument to the earlier Stonehenges , a massive commemoration (perhaps ceremonial) of the earlier site, perhaps like the erection of a cathedral rather than a small, more practical church. One thing is for sure: with its smaller ring diameter, Stonehenge III is less accurate than its predecessors.

The basic Stonehenge plan is illustrated above, where north is straight up, east is to the right. The outer sarcen ring surrounds the inner 5 trilithons, which open up to the northeast. Lighter-grey colored stones are toppled, broken, or missing. Darker stones have been restored by archaeologists. FYI, more detailed maps of Stonehenge I and II, and III are included at lab's end (note that north is slanted left in these additional diagrams).

Procedure

Let us design a few Stonehenge-like plans for different places on Earth. For this we will use two methods: (1) seat-of-the pants using our solar motion demonstrators, and (2) using a calculator. Using a protractor, we will sketch lines of sight for midsummer (summer solstice) sunrise and sunset and midwinter (winter solstice) sunrise and sunset.

First, review the behavior of the sun during the year by filling in the following table.

Celestial Sphere Coordinates of the Sun

Date Name Right Ascension (hours) Declination (degrees north or south)
March 21 Spring Equinox


Summer Solstice


Autumn Equinox

Dec. 21


We will use the earthbound coordinate system of altitude and azimuth. Altitude measure the angle of an object in degrees above the horizon. So an object on the horizon has an altitude of 0 degrees, and an object straight overhead at the zenith has an altitude of 90 degrees. Azimuth is usually measured starting at North and increasing toward the East, so that an object due East has azimuth 90 degreees, and object due south has an azimuth of 180 degrees, and an object due west has an azimuth of 270 degrees.

Write some azimuths around the green portion of your solar motion demonstrator. Fill in the following table using your solar motion demonstrator tool. Each tick represents 10 degrees. Try to estimate the azimuths to the nearest degree. The Keck telescope is located on the big island of Hawaii.

Sunrise/set azimuths using solar motion device

Location Latitude Az. of summer sol. sunrise Az. of winter sol. sunrise Az. of summer sol. sunset Az. of winter sol. sunset
Equator 0.0



Pullman
 46.8



Stonehenge 51.2



Anchorage
 60.5



Next, upack your calculator and try the following formula.

sin D = sin o / cos L

Where

When you have computed sin D, just hit the inverse-sin button to get the answer.

Refined azimuths using trig. formula

Location Latitude D (from formula) Az. of summer sol. sunrise (90-D) Az. of winter sol. sunrise (90+D) Az. of summer sol. sunset (270+D) Az. of winter sol. sunset (270-D)
Equator 0.0




Pullman
 46.8




Stonehenge 51.2




Anchorage
 60.5



The formula assumes a perfectly flat horizon. Q1: How do the numbers in the second table compare with the numbers in the first? (Approximately, by how many degrees do the two estimates differ, on average?)

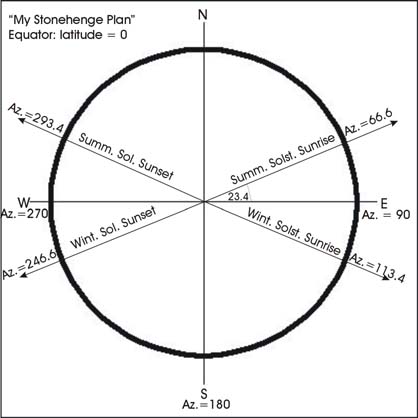
Next, using a ruler and protractor, sketch in lines of sight for the following observatory plans for each of 4 phenomena listed in the above tables. The first one, for the equator, is done for you, as a model.

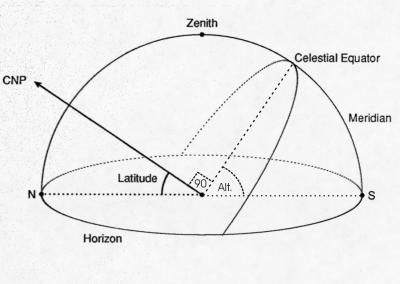
Finally, note that, as in the figure below, if you look north, at the celestial north pole (CNP), the altitude of the CNP above the horizon is the same as the observer's latitude. (This checks for the equator, where the CNP is right on the horizon, and for the north pole, where the CNP is exactly overhead). Furthermore, the angle between the CNP and the celestial equator must always be 90 degrees. So if the sun is on the celestial equator then its noontime altitude can be found by adding all the angles: (Latitude) + (90) + (Sun Alt.) = (180).

N. Celestical Pole and celestial hemisphere figure


Noontime sun altitudes

Location Latitude Alt. of spring equinox noon sun Alt. of summer solstice noon sun Alt. of fall equinox noon sun Alt. of winter solstice noon sun
Equator 0.0



Pullman 46.8



Stonehenge 51.2



Anchorage 60.5



The builders of Stonehenge originally found that the sun reached the same spot on the horizon at midsummer by patient observation over several years. It must have been quite a discovery for these stone-age tribesmen! In your writeup, tell how you could (Q2) find north, (Q3 ) find your present latitude, and (Q4) set up a (small) stonehenge that would point to the rising and setting suns at the equinoxes and solstices. You can use measurement devices like a protractor, string, astrolabe (a protractor with a plumb-bob attached), and your solar-motion demonstrator, but you have to be able to do the job in a few days or nights - you can't wait years to see where the Sun actually goes.

stonehenge map

Figure: The early Stonehenge. The illustration shows several stages of construction at the site. The first of these, "Stonehenge I," is an earthwork ring about 100m in diameter and 2m high. Its completeness was broken (as of about 2400 BC) by a single gap directed in the approximate direction of an outlying marker called the Heel Stone. In this gap, excavation has uncovered a grid of post holes: the remains, it seems, of an effort to mark the northernmost excursion of the moon. Note that the Heel Stone lies slightly away from a line drawn from the center of the earthwork ring to the horizon point marking the midsumer (solstitial) sunrise; in 2400 BC the Heel Stone was presumably more erect, and thus the alignment was more nearly perfect. Stonehenge I also included a circle of chalk-filled holes now named after John Aubrey. At some later time, Stonehenge II was added. It comprises two mounds of earth, covering some of the chalk-filled holes, and also the so-called station stones. As shown in the illustration, these additions to the site mark out the corners of a rectangle whose sides and diagonal align with various risings and settings of the sun and moon. In about 2100 BC, Stonehenge III was constructed at the center of the site (shown by the circle of dashes). Stonehenge III is the megalithic structure that draws our attention to the site today. [From "The Great Copernicus Chase" by Owen Gingerich, 1992, Sky Publishing Corp.]